СЕКЦИЯ ИНФОРМАТИКИ: Способы сжатия изображений на платформе IBM PC и, в частности, новый формат графических файлов RC1

Оглавление

• Введение
• Приложение 1. Метод Шеннона-Фэно.
• Приложение 2. Метод Хаффмана.
• Приложение 3. Формат файла RC.

Введение

В предлагаемом докладе приводится краткий обзор основных форматов графических файлов на платформе IBM, в том числе на основе вейвлетов и фракталов, исследования, проведенные в ходе разработки формата, результаты работы.

Основные задачи, которые стоят перед разработчиками новых форматов графических файлов:

1. Сделать так, чтобы сохраненное изображение занимало возможно меньший объем.
2. Сохранить при этом максимально возможное качество.

Признанным лидером по качеству является формат BMP - в этом формате просто не предусмотрено изменение сохраняемого изображения. Однако за это приходится расплачиваться неприемлемо большими объемами файлов, так как на каждую точку изображения приходится по 24 бита. Правда, существуют модификации формата, где на одну точку приходится 1, 4, 8 и 16 битов, но при этом палитра ограничивается соответственно 2, 16, 256 и 65536 цветами, то есть, происходит ухудшение изображения.

Наиболее популярными в настоящее время являются форматы GIF и JPEG.

Оба эти формата имеют как свои преимущества, так и свои недостатки.

В формате GIF [1] любое изображение переводится в состояние, когда на картинке остается не больше 256 различных цветов, которые заносятся в палитру и кодируются по методу Хаффмана [15] - то есть каждому индексу (номеру цвета в палитре) сопоставляется свой код, который тем короче, чем чаще встречается этот цвет/индекс.

Достоинства этого формата очевидны: малый объем конечного файла и хорошая контрастность изображения, что является результатом достаточно неплохого алгоритма преобразования цветов (глаз практически не ощущает разницу между исходным и преобразованным изображениями при больших разрешениях, когда единичный элемент изображения достаточно мал).

Недостатком же этого формата является ограничение в 256 "реальных" цветов и, как следствие, невозможность сохранять изображения в первоначальном виде.

Формат JPEG [1], напротив, изначально разрабатывался для полноцветных, 24-х битовых изображений. Особенность, использованная в этом формате - наличие в изображении больших участков, где наблюдается очень малая разница между цветом конкретной точки и общим фоном участка.

Чтобы сохранить изображение в качестве JPEG-файла, необходимо применить к нему дискретное косинусное преобразование (ДКП). Но затраты на ДКП больших участков изображения недопустимо велики, поэтому приходится разбивать рисунок на квадратные блоки со стороной 8 точек. После применения ДКП становится возможным в малом объеме сохранить почти все изображение, пренебрегая лишь незначительными деталями.

Достоинства: малый объем файла, зачастую меньше, чем у GIF.

Недостатки: плохая передача резких границ, заметные границы блоков, наличие различных артефактов (например, появление искажений ровного однотонного фона).

Одним из набирающих известность форматов является WVL или сохранение изображений на основе применения вейвлетов [2-6].

Вейвлет - функция, интеграл которой на всей числовой прямой равен 0, наибольшее значение достигается в 0, а при значении аргумента, стремящемся к бесконечности, быстро убывает. Используя масштабирование вейвлета, при котором он сжимается в A раз по вертикали и во столько же раз растягивается по горизонтали и его перемещение в нужную точку, находят сумму всех произведений соответствующих значений масштабированного вейвлета на значения анализируемой функции. В результате, по малому количеству этих сумм можно достаточно точно восстановить исходную функцию. В настоящее время готовятся к выходу форматы JPEG2000 [13] и MrSID [16], в которых как раз и используются вейвлеты.

Достоинства: малый объем файла, хорошая передача качества изображения.

Уже достаточно давно известны фракталы [14] - самоподобные множества, открытые Мандельбротом, задающиеся достаточно простой формулой. Идея такого сохранения заключается в применении к небольшому участку изображения стандартизованных операций (поворот, отражение, масштабирование, сдвиг) для получения всего изображения.

Достоинства: очень малые объемы, особенно на изображениях природы (лес, ландшафт, карты местности).

Недостатки: отсутствие общепризнанного стандарта, вычислительная сложность алгоритма.

Предлагаемый формат, названный RC1 (Rectangle Coder #1), как и формат JPEG, опирается на то, что практически в каждом изображении существуют большие участки одного или близких цветов, но имеющие неправильную границу. В связи с этим можно разбить эти участки на меньшие, но уже стандартизованные, то есть треугольники, квадраты, прямоугольники. При разработке формата вариант с треугольниками был отвергнут, так как при таком подходе изображение очень трудно разбить на необходимые области, что связано с "пиксельностью" изображения, то есть делением изображения на точки-"пиксели". По этим причинам программно были реализованы только варианты с разбиением на квадраты и на прямоугольники.

Преимущество квадратов и прямоугольников в том, что в этом случае необходимо передавать лишь цвет, ширину и высоту (для прямоугольников), либо только цвет (средний цвет всех точек области) и ширину (для квадратов), а координаты текущей считываемой области можно узнать из ранее переданной информации. Также преимуществом является возможность очень легко выделить непересекающиеся области.

Изначально предлагалась система обхода изображения построчно, то есть левый верхний угол очередного квадрата находится в самой левой незадействованной точке самой верхней не полностью заполненной строки. Например, на рисунке №1 показано, где должен находиться следующий квадрат. Положение следующего квадрата указано стрелкой.

При разбиении на квадраты рассматривались варианты с квадратами, стороны которых являлись степенями простых чисел или произведениями степеней простых чисел от 2 до 13. В результате ряда тестовых испытаний было выяснено, что оптимальным является случай, когда используются только квадраты со стороной выраженной степенью числа 2.

Сначала предлагалась система, по которой из картинки "вырезаются" квадраты с максимально возможной из этой точки стороной (длина стороны равна 2n), а затем каждый из этих квадратов делится на 4 равных меньших квадрата и так далее, пока все точки квадрата не будут иметь достаточно близкие цвета. На рисунке №2 показан пример разбиения одного из квадратов.

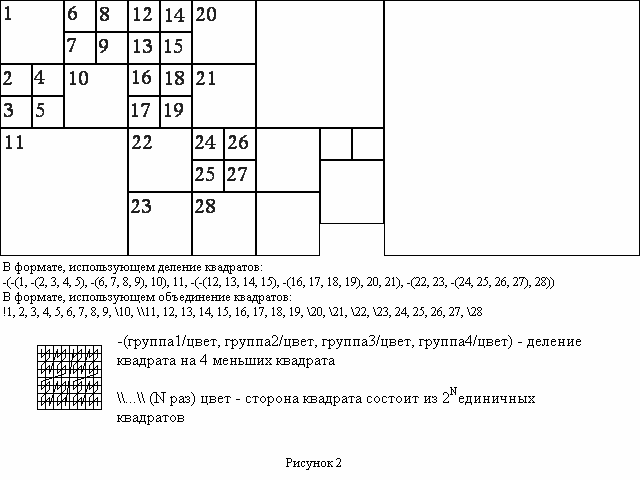
После нескольких экспериментов стало ясно, что можно значительно выиграть во времени сохранения и прочтения картинки, если модернизировать систему позиционирования. Для этого необходимо лишь представить картинку вписанной в квадрат, а уже этот квадрат рекурсивно разбивать, как было показано в предыдущем случае. Таким образом, используя рекурсивные процедуры на каждом шаге можно определить точку, из которой должен выходить следующий квадрат. Этот способ также сокращает затраты памяти, так как не требуется хранить массив, где отмечается, какие точки уже использованы. Этот способ обхода показан на рисунке №2. То есть точки проходятся в той очередности, как они соединены, начиная с левой верхней. Если точка еще не занята, то из нее "нарезается" квадрат.

После ряда тестов выяснилось, что если не делить квадраты от максимальных к единичным, а, наоборот, объединять соседние квадраты по 4, начиная с единичных, пока все точки в квадратах близки по цвету, то можно значительно сэкономить объем файла, так как в большинстве изображений требуется сохранять очень много указателей деления, но указателей объединения намного меньше. Например, чтобы "добраться" до квадрата 8х8 на картинке размером 256х256, требуется 5 указателей деления (256->128->64->32->16->8) и лишь 3 указателя объединения (1->2->4->8).

При делении изображения на квадраты большим преимуществом является то, что такой способ сохранения может быть очень легко распараллелен [10-12], а это значительно ускорит запись и чтение изображений.

Однако такой способ имеет один недостаток - каждый раз объединяемые квадраты должны "укладываться" в двоичную сетку. То есть квадраты №4 и №5 могут принадлежать одному квадрату со стороной 2, а квадраты №4 и №7 - не могут.

В конечном итоге, был реализован вариант, в котором изображение делится на прямоугольники со сторонами 2m и 2n. Это позволило записывать в файл лишь ширину (m записей), высоту (n записей) и цвет (1 запись). Размер каждой записи определяется в зависимости от изображения с помощью алгоритма Шеннона-Фэно, минимизирующего общий объем конечного файла. Координаты прямоугольника не требуется передавать, так как они могут быть определены на основе уже известной информации.

В этом способе из текущей точки "нарезается" прямоугольник максимально возможной площади. Для того, чтобы не хранить массив уже использованных точек и сохранить возможность использования рекурсивных процедур, пришлось пойти на некоторые ограничения. Например, прямоугольник не может иметь точку в какой-либо строке, если самая нижняя из занятых точек столбца, находящегося слева от "точки нарезания" находится выше этой строки, и, аналогично, для правой границы и строки сверху от "точки нарезания" (считается, что прямоугольник, прилегающий к верхней стороне не ограничен справа, а прилегающий к левой стороне - снизу). В результате можно вместо массива MxN использовать два массива общего объема M+N. Такой способ приводит к образованию разбиений показанных на рисунке №3. Например, прямоугольники №14 и №18 не могли быть объединены, так как на тот момент еще не существовал прямоугольник №17.

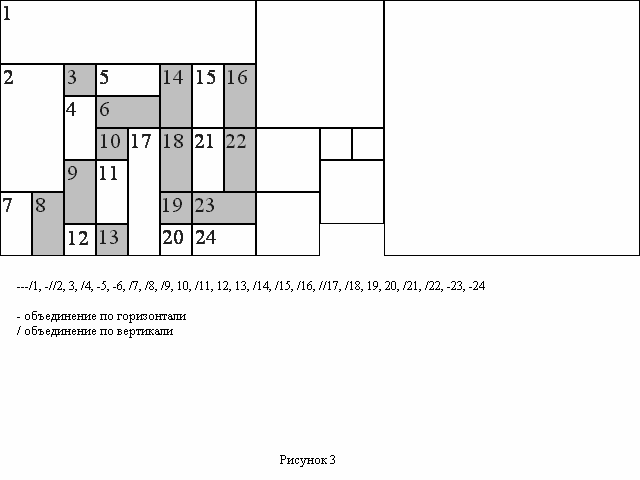
После таких преобразований, на выходе алгоритма, получаем группы из нескольких (возможно ни одного) указателей объединения по горизонтали, указателей объединения по вертикали и цвета. После этого, используя заданные пользователем параметры, производится преобразование цветов. Пользователь может задать качество итогового изображения, варьируя различные параметры: количество бит на красную, зеленую и синюю цветовые составляющие, максимальный допустимый разброс оттенков внутри одной области. Если пользователь указал в качестве допустимого большее число бит, чем реально требуется на кодирование какой-либо цветовой составляющей, то это количество автоматически уменьшается.

Полученные цвета кодируются по методу Шеннона-Фэно [9] (дающим лучшие, по сравнению с уже упоминавшимся способом Хаффмана, результаты), то есть более часто встречающимся цветам ставятся в соответствие более короткие коды. В этом случае, по крайней мере однажды необходимо записать цвет в виде R+G+B+A, где каждая буква - количество бит на соответствующую составляющую, чтобы сопоставить код с каким-либо конкретным цветом. По этой причине иногда бывает выгоднее писать цвет всегда в виде R+G+B+A и не включать этот цвет в число кодируемых (если длина соответствующего кода больше R+G+B+A).

Отличительными особенностями предлагаемого формата являются:

1. Гибкая настройка качества и объема изображения, в отличие от GIF и JPEG.
2. Возможность сохранения без искажений, но со значительным уменьшением объема.
3. Четкая передача резких границ.
4. Полная поддержка полноцветных 24-битных изображений.
5. Возможность записи и чтения 32-битных изображений (8 дополнительных бит на Alpha-составляющую, отвечающую за прозрачность точки).
6. Возможность передавать дополнительную информацию (например, частные отклонения от общего фона) в изображениях, где Alpha-составляющая не используется.
7. Нефиксированная процедура перекодирования изображения - форматом определяется лишь вид конечного файла, но сами процедуры кодирования всегда могут быть изменены для улучшения, в отличие от жестко заданных процедур форматов GIF и JPEG.

Примерное расположение форматов RC, GIF, JPEG и BMP на графике качество-объем показано на рисунке №4.

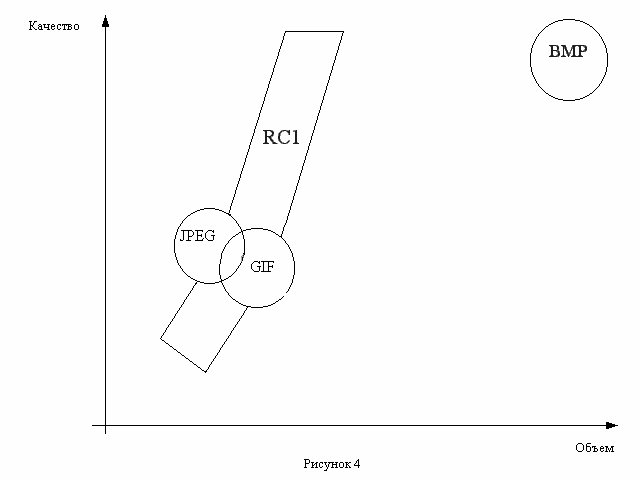
Демонстрация формата осуществляется с помощью программы, созданной на Borland Delphi 4, в операционной системе Windows 95/98. Программа позволяет считывать изображения в форматах RC1, BMP, WMF и ICO, и записывать их в форматах RC1 и BMP.

Для определения качества используется программа, находящая разницу между исходным и преобразованным изображениями. Очевидно, что чем меньше эта разница и чем ближе она сконцентрирована вокруг резких деталей изображения, тем лучше воспринимаемое качество.

В приложении приведены алгоритмы подбора кодов по Хаффману и Шеннону-Фэно, а также детально описанный формат файла RC1.

Приложение 1. Метод Шеннона-Фэно.

Изначально все коды - пустые.

1. Все элементы, содержащиеся в файле, (в нашем случае - цвета) сортируются в порядке убывания частоты появления этого элемента в файле.
2. Если в наборе лишь один элемент, то осуществляется переход к пункту 6.
3. Определяется точка деления такая, что вероятность появления в файле любого элемента, стоящего слева от точки деления, приблизительно равна вероятности появления в файле любого элемента, стоящего справа от точки деления.
4. К кодам всех элементов, стоящих слева от точки деления, приписывается 0, а у стоящих справа - 1.
5. Операции повторяются, начиная со второй, используя в качестве входных данных элементы от начала набора до точки деления и от точки деления до конца набора.
6. Когда всем элементам сопоставлены двоичные коды, алгоритм завершает свою работу.

Приложение 2. Метод Хаффмана.

Изначально все коды - пустые.

1. Выбираются два наименее часто встречающиеся элемента.
2. К коду одного из элементов приписывается 0, другого - 1.
3. Эти элементы объединяются в один, вероятность появления которого равна сумме вероятностей этих элементов.
4. Операции повторяются, начиная с первой, пока не останется лишь один элемент.

Приложение 3. Формат файла RC.